联言命题及联言推理
复合命题及其推理概述
复合命题是在自身中包含了其它命题的命题。
井冈山的夜晚是动人的,井冈山的早晨就更加美丽了。
构成复合命题的命题叫支命题,用p、q、r、s等表示。
将支命题结合起来的概念叫联结项。
根据联结项的不同,我们把复合命题分为四种类型:
复合命题推理是以复合命题为前提或结论所构成的演绎推理。
该案件的作案人或者是甲或者是乙,现查明该案件的作案人不是甲,所以该案件的作案人是乙。
联言命题及联言推理
联言命题的定义、结构及形式
联言命题是断定几种事物情况同时存在的复合命题。
(1)他不但是语言的巨人,而且是行动的高标。
(2)时间就是速度,时间就是力量、时间就是生命在结构上,联言命题由联言支和联言联结项构成。
联言命题的逻辑形式为
p并且q
或者
p^q(“^”读作“合取”)
联合命题的逻辑性质
全部为真则为真,否则为假。

联言支的顺序安排
一般情况可以换位而且意义不变。
李白是诗仙,杜甫是诗圣。
有时虽然能够换位,但是意思有所变化。
情有可原,理无可恕。
联言推理
- 分解式:
- 组合式:
在桌子上有三张扑克牌,排成一行。
现在我们已经知道:
(1)K右边的两张牌中至少有一张是A;
(2)A左边的两张牌中也有一张是A:
(3)方块左边的两张牌中至少有一张是红心:
(4)红心右边的两张牌中也有一张是红心。
请问:这三张牌从左到右依次是什么牌?
解析 :
根据前两个条件,可推出三张牌是:KAA;
根据后两个条件,可推出三张牌是:红红方:
综合牌点与花色,三张牌是:红K,红A,方A。
选言命题及选言推理
选言命题
选言命题是断定事物存在若干可能情况的复合命题。
(1)学习不好的原因,或者是基础差,或者是不努力,或者是不得法。
(2)蜜蜂要么是蜂王,要么是雄蜂,要么是工蜂。
选言命题由选言支和选言联结项构成。
相容选言命题
-
特点:选言支至少一真
他或者是诗人,或者是画家。
-
逻辑形式
或者p,或者q
或者
pVq
(“V”读作“析取”) -
联结项:或者……或者……、也许……也许……
-
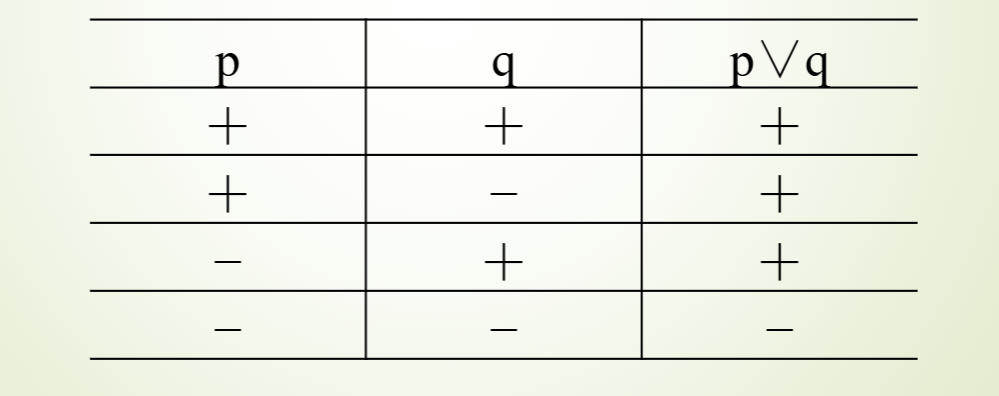
相容选言命题的逻辑性质
一真则真,全假则假。
不相容选言命题
-
特点:选言支恰有一真
要么老虎吃掉武松,要么武松打死老虎。 -
逻辑形式
要么p,要么q
或者
-
联结项:要么……要么……、或者……或者……二者必居其一
-
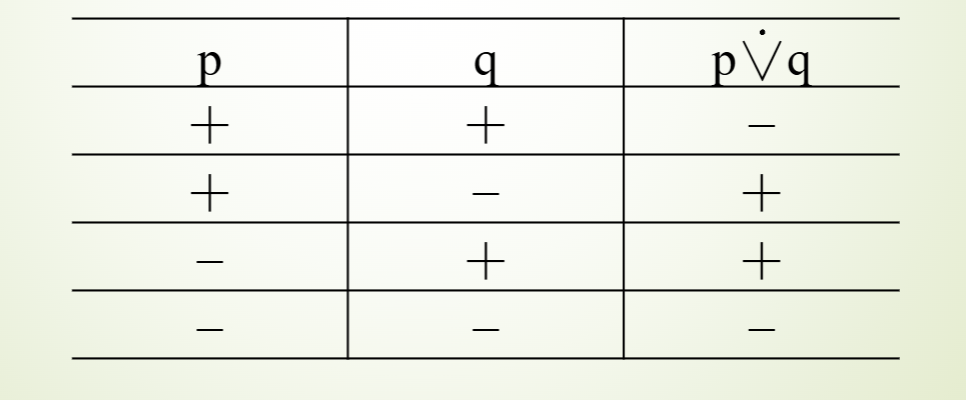
不相容选言命题的逻辑性质
同假异真
运用选言命题应注意的问题
(1)不要遗漏真实选言支。
执竿入城,遗漏前后纵向方案。
(2)分清相容选言命题和不相容选言命题,正确选用联结项。
他或者是教师或者是律师。
(3)分清选言命题和联言命题,正确选用联结项。
携带准考证、身份证或学生证。
选言推理


有三个电影厂的影片获了奖。包括甲厂的《黄河》、乙厂的《孙悟空》、丙厂的《白娘子》。三部影片的导演在授奖大会上见了面。
甲厂的导演说:“真是有趣得很我们三个的姓分别是片名的第一个字。”
丙厂的导演说:“我们每个人的姓同本厂片名的第一个字又不一样。”
一个姓孙的导演笑一笑说:“真是这样。”
请问:这三部影片的导演各姓什么?
答案:甲厂姓孙,乙厂姓白,丙厂姓黄。
选言命题和联言命题转换

假言命题
小张约小李第二天去商场,小李说:“如果明天不下雨我去爬山。”第二天,天下起了毛毛细雨,小张以为小李不会去爬山了,就去小李的宿舍找他,谁知小李仍然去爬山了待两人又见面时,小张责怪小李食言,既然天下雨了,为什么还去爬山;小李却说,他并没有食言,是小张的推论不合逻辑。对于两人的争论,以下哪项论断是合适的?
A.小张和小李的这个争论是没有意义的。
B.小张的推论不合逻辑。
C.两个人对毛毛细雨的理解不同。
D.由于小李食言,引起了这场争论。
答案:
假言命题就是断定某一事物情况存在是另一事物情况存在的充分条件或必要条件的复合命题。
(1)如果物体摩擦,那么它就会生热。
(2)一个人只有充满自信,他才具有创造性。
假言命题有两个假言支,表示条件者叫前件,依赖条件而成立者叫后件。假言命题一般用假设复句、条件复句表达。
充分条件假言命题
-
定义
充分条件假言命题是断定某一事物情况存是另一事物情况存在的充分条件的假言命题。(1)如果两个角是对顶角,则两个角相等。
(2)只要某人犯罪,那么他一定违法。所谓“充分”就是“有此足够”的意思。
-
逻辑形式
或者
-
常用的联结项
“如果……那么……” “只要……就……” “若……则……”等。 -
逻辑性质
当前件真而后件假时该命题假,其余情况下,该命题都真。这种性质可用下表来表示:

