简单命题及其推理

命题推理概述及直言命题

命题：可以判断真假的陈述句。

命题要用语句表达，但二者之间具有不对应性。

1. 有的语句表达命题，有的语句不表达命题

   陈述句表达，祈使句不表达。疑问句和感叹句有的表达，有的不表达。

2. 有的语句可以表达不同的命题

   (1)他老得连我都认不出了。(双层含义，老糊涂了还是，容貌变老)
   (2)侦察员在屋顶上发现了敌人。（侦察兵在屋顶上发现了那里的敌人没表达出来）

3. 有的命题可用不同的语句来表达

   (1)我是一个学生。
   (2)|am a student.

命题的种类

推理概述

推理就是根据已知命题推出一个新命题的思维形式。

任何推理都是由前提、结论两部分构成的。
我们把作为推理根据的已知命题称为前提。
把根据已知命题推出的新的命题称为结论。
而前提和结论之间的逻辑联结方式，叫推理形式，

(1)小说是文艺作品所以，有的文艺作品是小说。
(2)所有的商品都是劳动产品，电视机是商品，所以电视机是劳动产品。

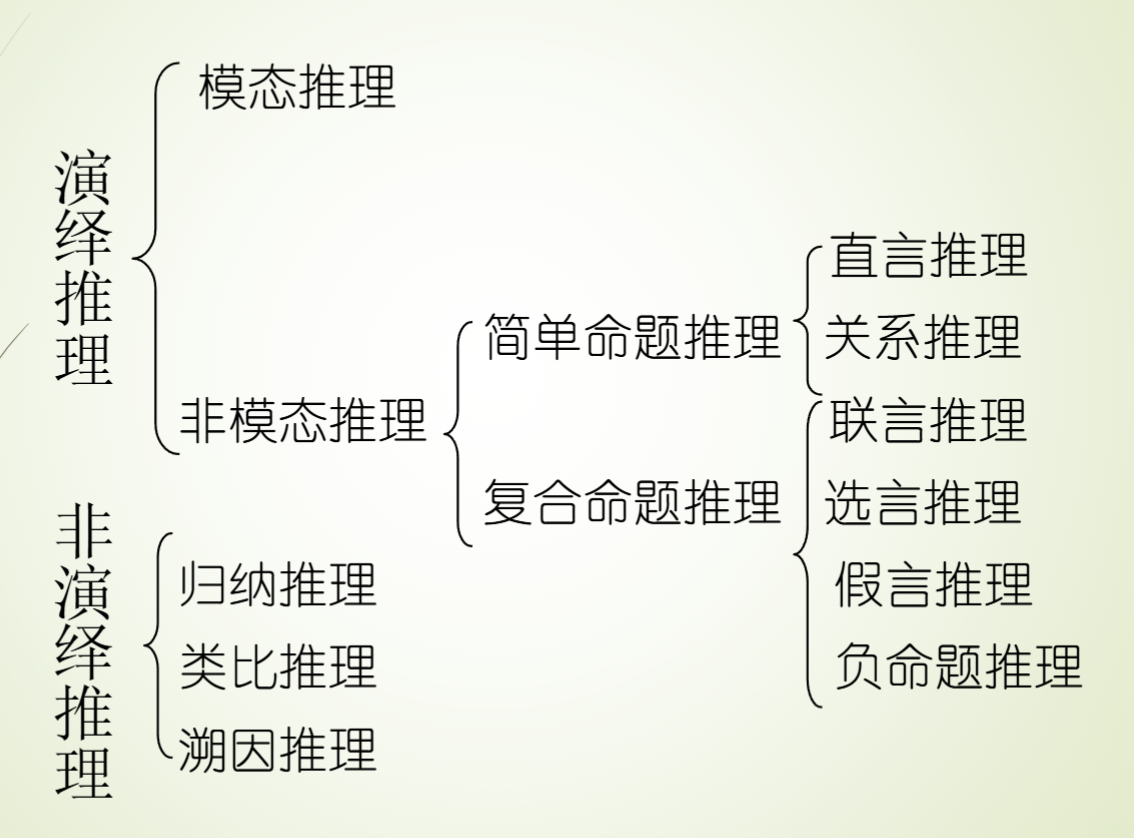
推理的种类

前提、形式对结论的影响

前提	形式	结论
真实	有效	必然真
真实	无效	可能假
虚假	有效	可能假
虚假	无效	可能假

逻辑学中，常常用有效性来评价演绎推理，用可靠性评价非演绎推理。

直言命题

直言命题是一种简单命题，它是断定事物具有或不具有某种性质的命题，也叫做性质命题。例如:

(1)所有的知识分子都是脑力劳动者。
(2)我班所有的同学都不是党员。
(3)有些鸟是会飞的。
(4)有些植物不开花。

任何一个直言命题都由主项、谓项、联项和量项四个部分组成。
主项:S(subject)
谓项:P(predicate)
联项:是、不是
量项:所有、有的、某个

直言命题的量项

量项有三种情况:全称、特称和单称。
①全称量项。全称量项常用的语词是“所有”“凡是”“一切”它表示直言命题对主项中的每一个个体都做了断定。全称量项有时会省略。

②特称量项。特称量项常用的语词是“有的”“有些”“至少有一个”等，它表示直言命题对主项中的至少一个个体做了断定。特称量项不能省略。

③单称量项。当主项为单独概念时,单称量项不出现,当主项是普遍概念时，单称量项常用的语词是“这个”“那个”等，它表示直言命题对主项中的某个个体做了断定。

特称命题所断定的主项的数量是不确定的，它只是断定至少有一个S如何，不意味着有S不如何

直言命题的类型

根据联项和量项的不同结合,可将直言命题分为以下六种基本形式。
(1)全称肯定命题。逻辑形式:所有S是P。简称SAP，又称A。
(2)全称否定命题。逻辑形式:所有S不是P。简称SEP，又称E。
(3)特称肯定命题。逻辑形式:有S是P。简称SIP，又称I。
(4)特称否定命题。逻辑形式:有S不是P。简称SOP，又称O。
(5)单称肯定命题。逻辑形式:某个S是P。简称SaP。又称a。
(6)单称否定命题。逻辑形式:某个S不是P。简称SeP。又称e。

直言命题的真假

直言命题的真假取决于主谓项之间的关系。
（这里之分析典型的A、E、I、O四种命题）

S与P关系	全同关系	真包含于关系	真包含关系	交叉关系	全异关系
SAP	+	+	-	-	-
SEP	-	-	-	-	+
SIP	+	+	+	+	-
SOP	-	-	+	+	+
+ 代表真 - 代表假

直言命题直接推理

直接推理是以一个已知命题为前提，推出另一个新命题作为结论的推理。
直言命题直接推理就是以一个己知的直言命题为前提，根据直言命题的性质推出结论的推理。
它分为两种:一是直言对当关系推理，一是直言变形推理。

直言对当关系推理

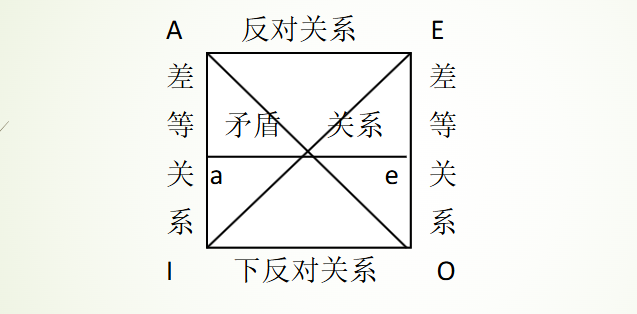
矛盾关系：一真一假；
反对关系：至少一假；
下反对关系：至少一真；
差等关系：上真下就真，下假上就假；

矛盾关系推理

矛盾关系推理存在十种有效形式：

反对关系推理

下反对关系推理

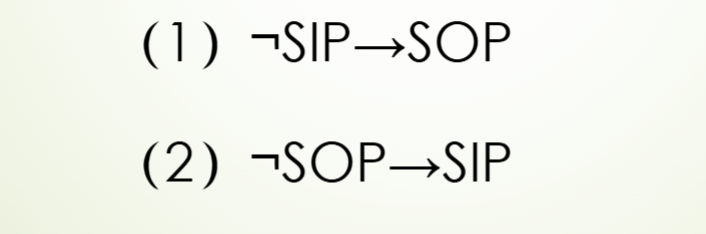
差等关系推理

直言变形推理

换质推理

换质推理必须遵守的规则：

1. 改变前提的联想。
2. 结论中的谓项要与前提中的谓项相矛盾。

$$SAP \to SE\bar{P}$$

所有恒星都是发光体所以所有恒星都不是非法关系。

$$SEP \to SA\bar{P}$$

所有的塑料制品都不是玻璃制品，所以所有塑料制品都是非玻璃制品。

$$SIP \to SO\bar{P}$$

有的物体是导体，所以有的物体不是非导体。

$$SOP \to SI\bar{P}$$

有些被告不是有罪的，所以有些被告是无罪的。

换位推理

换位推理必须遵守的原则：
（1）调换前提中主、谓项的位置。
（2）在前提中不周延的概念在结论中也不得周延。

周延与不周延？
在一个直言命题中，如果其主项或谓项的全部外延都被判定，那么，他就是周延的。否则，就是不周延的。

判断条件：
直言命题的主项是否周延看量项：
全称命题的主项是周延的。
特称命题的主项是不周延的。

直言命题的谓项是否周延要看联项；

肯定命题的谓项是不周延的。
否定命题的谓项是周延的。

首先看主项是全称命题则是周延的负责不周延，其次看谓项如果联项是否定则周延否则不周延。

$$SAP \to PIS(变量换位)$$

所有的树都是植物，所以有的植物是树。

$$SEP \to PES(变量换位)$$

凡行星都不是发光体，所以凡发光都不是行星。

$$SIP \to PIS(变量换位)$$

有的青年是学生，所以有的学生是青年。

$$SOP （不能换位）$$

有的计算机不是微型计算机，所以？

直言命题间接推理————三段论

三段论的含义及构成

三段论是由两个含有一个相同变项(中项)的直言命题作前提，另一个直言命题作结论组成的直言命题间接推理。

所有的鸟都是有羽毛的，燕子是鸟，所以燕子是有羽毛的，

三段论有且只有三个变项，结论中的主项称为小项，通常用S表示;
结论中的谓项叫大项，通常用P表示;
两个前提共有的概念叫中项，通常用M(medium媒介物)表示。

三段论由三个直言命题构成,其中包含有大项的前提是大前提，包含有小项的前提是小前提，由两个前提推出的命
题是结论。

三段论的格与式

由于中项位置的不同又四种:

三段论的逻辑形式，习惯上是大前提居前，小前提居中，结论居后。
三段论中的三个命题可以是任意一种直言命题。A、E、I、O四种命题在三段论中的不同组合形式，叫做三段论的式。

式的名称顺序是:

大前提+小前提+结论

三段论的基本规则

规则1:中项至少周延一次。违反这条规则，就会犯“中项两次不周延”的错误。

规则2:在前提中不周延的概念在结论中也不得周延违反这条规则，就会犯“大项(或小项)不当周延，的错误。

规则3:前提与结论中否定命题的数量相等。违反这条规则，就会犯“前后否定数量不等”的错误。

三段论的省略形式

任何一个三段论都由大前提、小前提和结论三个直言命题组成。

但在实际表达时，为了简洁，人们往往省略其中一个不言而喻的命题，这就是省略式的三段论。

省略式的三段论可以复原。复原时注意以下几个问题:

第一，确保三个变项分别出现两次。
第二，根据基本规则确定补充命题的变项位置、联项类型和量项类型。
第三，尽量按照大前提、小前提、结论顺序排

现在我们回看一下开头的那个省略式的三段论:
有些导演留大胡子，因此有些留大胡子的是大嗓门。

为使上述推理成立，必须补充什么样的前提?
按照刚才强调的复原要领，操作一下

第一，确保三个变项分别出现两次。
三个变项分别是:导演、留大胡子、大嗓门。
其中，“留大胡子”是小项，已经出现两次，无需再补充。
“导演”是中项，“大嗓门”是大项，它们分别只出现一次，还应该再分别补充一次。

第二，根据基本规则确定补充命题的变项位置、联项类型和量项类型。
现在我们要考虑的是:“导演”“大嗓门”如何组成一个合适的命题。
根据基本规则3“前提与结论中否定命题的数量相等”，补充的命题应该是肯定命题。
根据规则1“中项至少周延一次”，“导演”应该至少周延一次，现有的“导演”是特称命题的主项，不周延，那么补充的
“导演”必须周延。
而补充的命题已经确定为肯定命题，那么“导演”若要周延，必须做主项，而且这个命题必须是全称的。
因为如果做不到这两点，那么“导演”无法周延。
综上所述，补充的前提应该是：
所有的导演都大嗓门。

关系命题及关系推理

关系命题的定义

甲:你昨夜梦见我没有?
乙:没有。
甲:我分明梦见你，还与你说了许多话，你怎么说没有梦见我?
乙:岂有此理?难道你梦见我，我就会梦见你吗?
从对话中可以看出，甲的思维出了问题，那么到底是什么问题呢？

关系命题的定义

关系命题也是一种简单命题，它是断定对象之间具有或不具有某种关系的命题。

(1)程遥和路远是朋友。
(2)小王和小李不是同乡。
(3)小芹喜欢小二黑。
(4)小红不认识小白。

关系命题的结构

关系命题由“体项”“关系项”“量项”“联项”四个部分组成。

我们以“有些学生不了解所有外国作家”做分析。

体项，一般称为关系者项。它是关系命题中表示所断定的对象的概念，也就是关系的承担者，具有实体性。类似直言命题中的主项，但至少有两个，通常用a、b、c等表示。如例中的“学生”“外国作家”。 关系项。它是关系命题中表示对象之间或有或无的某种属性的概念。类似直言命题中的谓项。一般用R(relation)表示。如例中的“了解”。 量项。它是关系命题中表示对象数量范围的概念。与直言命题中

的量项相同，但可以有多个。如例中的“有些”
“所有”。

联项。它是关系命题中表示对象之间是否存在关系的概念。与直言命题中关系是否存在的概念。肯定联项常常不出现，但否定联项必不可少。如例中的“不”。

关系命题的种类

体项至少有两个，可分为二元和多元两种。
关系项可以由动词或名词充当。
量项有全称、特称、单称三种。
联项有肯定、否定两种。

根据体项和联项的结合情况，可以把关系命题分为四类：

二元肯定命题 逻辑形式:aRb。如:甲和乙是朋友。
二元否定命题 逻辑形式:aRb。如:A不等于B。
多元肯定命题 逻辑形式:aRbc。如:人立于天地之间。
多元否定命题 逻辑形式:aRbc。如:黑龙江不是位于吉林和辽宁之间。

关系的逻辑性质

(1)关系的对称性
对 称(一定如此，如:朋友)
反对称(一定不如此，如:大于)
非对称(不一定如此，如:梦见)
(2)关系的传递性
传 递(一定如此，如:高于)
反传递(一定不如此，如:比…高两公分)
非传递(不一定如此，如:邻居)

关系推理

对称性

条件:关系项具有对称的性质。
逻辑形式:

$${aRb} \over {\therefore bRa}$$

李白和杜甫同时代，所以，杜甫和李白同时代。

反对称性

条件:关系项具有反对称的性质。
逻辑形式:

$${aRb} \over {\therefore b\bar{R}a}$$

嵩山高于衡山，所以衡山不高于嵩山。

传递关系

$$aRb$$

$${bRc} \over {\therefore aRc}$$

孔子早于孟子，孟子早于荀子，所以，孔子早于荀子。

反传递关系

$$aRb$$

$${bRc} \over {\therefore a\bar{R}c}$$

老李和大李是父子，大李和小李是父子，所以，老李和小李不是父子。

混合关系推理

（1）肯定主体式

$$aRb$$

$$c是a \over {\therefore cRb}$$

(2)肯定课客体式

$$aRb$$

$$c是b \over {\therefore aRc}$$